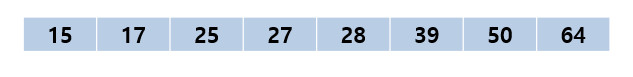기수 정렬 (Radix Sort)

목표

• Radix Sort에 대해 설명할 수 있다.
• Radix Sort 과정에 대해 설명할 수 있다.
• Radix Sort를 Python으로 구현할 수 있다.
• Radix Sort의 특징을 이해하여 시간 복잡도와 공간 복잡도를 계산할 수 있다.

요약

• Radix Sort는 낮은 자리수부터 비교하여 정렬해 간다는 것을 기본 개념으로 정렬하는 알고리즘이다.
• 비교 연산을 하지 않으며 정렬 속도가 빠르지만 데이터 전체 크기에 기수 테이블의 크기만한 메모리가 더 필요하다. (공간 복잡도가 높아진다.)

과정 (오름차순)

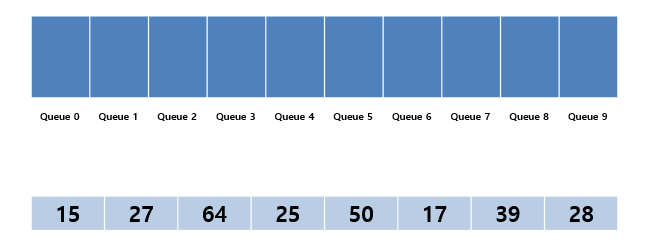
1. 0~9 까지의 Bucket(Queue 자료구조)을 준비한다.

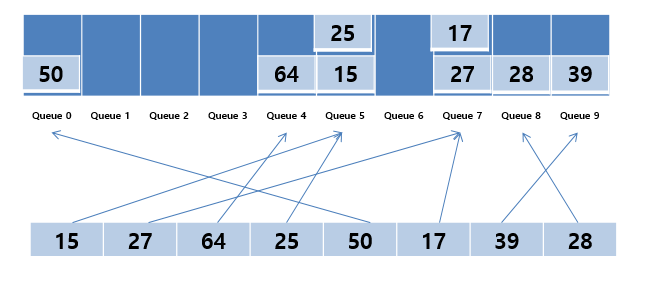
2. 주어진 데이터의 숫자를 보고 1의 자리수의 숫자에 해당하는 Bucket에 데이터를 넣는다.

3. Bucket 0부터 9까지 차례대로 데이터를 가져온다.

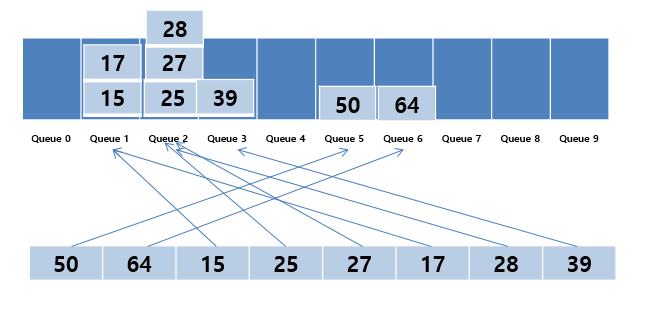
4. 다음은 10의 자리수의 숫자에 해당하는 Bucket에 데이터를 넣는다.

5. 역시 순서대로 데이터를 가져오면 정렬이 완료된다.

Python 코드

from collections import deque

def radix_sort(nums):
    buckets = [deque() for _ in range(10)]

    max_val = max(nums)
    Q = deque(nums)
    cur_ten = 1

    while max_val >= cur_ten:
        while Q:
            num = Q.popleft()
            buckets[(num // cur_ten) % 10].append(num)

        for bucket in buckets:
            while bucket:
                Q.append(bucket.popleft())

        cur_ten *= 10

    return list(Q)


print(radix_sort([15, 27, 64, 25, 50, 17, 39, 28]))

시간 복잡도

• 시간 복잡도는 O(d * (n + b))
  • d는 최대값의 자릿수, b는 배열의 최댓값(기수 정렬의 경우에는 10으로 고정되어 있다.)
  • Counting Sort의 경우 O(n + k)로 배열의 최댓값 k에 영향을 받는다.

공간 복잡도

기존에 주어진 배열에서 원소 Swap만 이루어지므로 공간 복잡도는 O(n)이다.

특징

장점

1. 자릿수가 고정되어 있어서 안정성이 있다.
2. 문자열, 정수 정렬이 가능하다.

단점

1. 자릿수가 없는 것은 정렬할 수 없다. (부동 소숫점)
2. 중간 결과를 저장할 bucket 공간을 만들기 위한 메모리가 더 필요하다.

Reference

• https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/Sort_Radix.md
• https://lktprogrammer.tistory.com/48