티스토리 뷰
목표
- Heap Sort에 대해 설명할 수 있다.
- Heap Sort 과정에 대해 설명할 수 있다.
- Heap Sort를 Kotlin으로 구현할 수 있다.
- Heap Sort의 특징을 이해하여 시간 복잡도와 공간 복잡도를 계산할 수 있다.
요약
완전 이진 트리를 기본으로 하는 힙(Heap) 자료구조를 기반한 정렬 방식
완전 이진 트리
삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리
힙(Heap)
부모 노드가 자식 노드보다 항상 작은 형태의 완전 이진트리(오름차순 기준)
삽입
- 아래와 그림과 같은 Heap이 있다고 하자. Heap의 삽입은 먼저 가장 끝의 노드에서 이뤄진다.
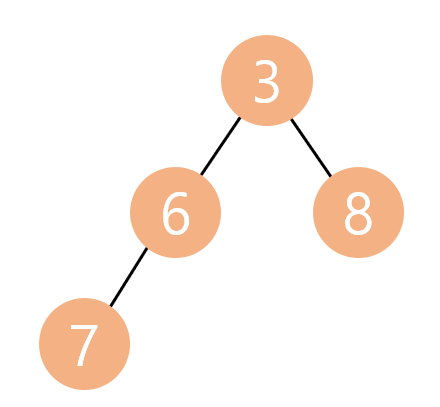
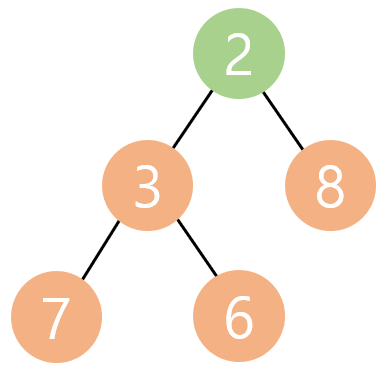
- 여기에 2를 추가하게 된다면 다음과 같이 추가된다.

- 부모 노드는 항상 자식 노드보다 작아야 한다. 새로 추가 된 2 노드의 부모 노드와 비교하여 2가 더 작으므로 위치를 교환해준다.

- 다시 2의 노드와 부모 노드인 3을 비교하여 2가 더 작으므로 위치를 교환한다.
삭제
- 힙의 삭제는 루트 노드에서 이뤄진다.

- 2 노드가 pop되어 삭제하고 마지막 노드(6노드)를 루트 노드로 옮긴다.
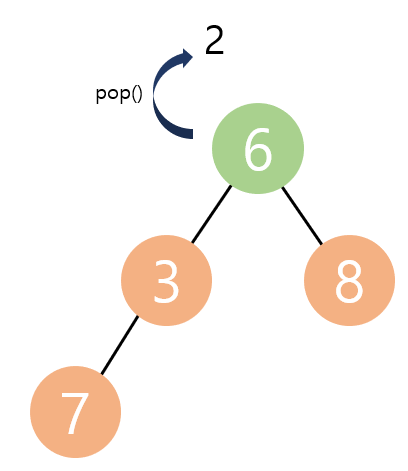
- 이제는 자식 노드 중에서 작은 요소와 바꿔준다. 이번 경우엔 3과 위치를 바꾼다.
- 다시 자식 노드인 7과 비교하고 7보다 작은 것을 확인하였으니 바꾸지 않고 종료한다.
정렬 과정 (오름차순, 최소 힙)
- 정렬해야 할 n개의 요소들로 이뤄진 최소 힙을 만든다.
- 한 번에 하나씩 요소를 힙에서 꺼내어 배열의 뒤부터 저장한다.
Kotlin 코드
fun heapSort(array: MutableList<Int>): List<Int> {
var results = mutableListOf<Int>()
// array 전체 길이 구함
var arrayLen = array.count()
// max heap 초기화
// 자식 노드를 가진 노드들만 순회
for (i in arrayLen / 2 - 1 downTo 0) {
heapify(array, arrayLen, i)
}
// 하나씩 추출
for (j in arrayLen - 1 downTo 0) {
results.add(array[0])
array[0] = array[j]
heapify(array, --arrayLen, 0)
}
return results
}
fun heapify(array: MutableList<Int>, heapSize: Int, pIdx: Int) {
// 부모 노드, 좌측 자식 노드, 우측 자식 노드 구함
var p = pIdx
var l = pIdx * 2 + 1
var r = pIdx * 2 + 2
// 왼쪽 자식 노드와 비교
if (l < heapSize && array[l] < array[p]) {
p = l
}
// 오른쪽 자식 노드와 비교
if (r < heapSize && array[r] < array[p]) {
p = r
}
// 부모 노드의 값보다 자식 노드의 값이 크다면 재귀함수
if (pIdx != p) {
val temp = array[p]
array[p] = array[pIdx]
array[pIdx] = temp
heapify(array, heapSize, p)
}
}시간 복잡도
삽입, 삭제
- 비교 노드의 인덱스가 1/2씩 줄어들기 때문에 시간 복잡도는 O(logN)이다.
- 리스트의 길이 (N) * 비교 연산 횟수(log N) = O(N logN)
특징
힙 정렬이 유용할 때
- 가장 크거나 가장 작은 값을 구할 때
- 매번 안정적이게 빠른 속도로 최대값이나 최솟값을 찾을 수 있다. => O(N logN)
- 최대 k 만큼 떨어진 요소들을 정렬할 때
- 삽입 정렬보다 더욱 개선된 결과를 얻어낼 수 있음
Reference
- https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/MergeSort.md
- https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
- https://nobilitycat.tistory.com/entry/%ED%9E%99Heap%EA%B3%BC-%EC%99%84%EC%A0%84-%EC%9D%B4%EC%A7%84-%ED%8A%B8%EB%A6%ACComplete-binary-tree
- https://codingdog.tistory.com/entry/%EC%99%84%EC%A0%84%EC%9D%B4%EC%A7%84%ED%8A%B8%EB%A6%AC-vs-%ED%8F%AC%ED%99%94%EC%9D%B4%EC%A7%84%ED%8A%B8%EB%A6%AC-%EC%9D%B4-%EB%91%98%EC%97%90-%EB%8C%80%ED%95%B4-%EC%95%8C%EC%95%84%EB%B4%85%EC%8B%9C%EB%8B%A4
반응형
'Programming > 알고리즘' 카테고리의 다른 글
| 계수 정렬 (Counting Sort) (0) | 2021.06.10 |
|---|---|
| 기수 정렬 (Radix Sort) (1) | 2021.06.10 |
| 합병 정렬 (Merge Sort) (0) | 2021.06.07 |
| 퀵 정렬 (Quick Sort) (0) | 2021.06.01 |
| 삽입 정렬 (Insertion Sort) (0) | 2021.05.30 |
댓글
