티스토리 뷰
목표
- Merge Sort에 대해 설명할 수 있다.
- Merge Sort 과정에 대해 설명할 수 있다.
- Merge Sort를 Kotlin으로 구현할 수 있다.
- Merge Sort의 특징을 이해하여 시간 복잡도와 공간 복잡도를 계산할 수 있다.
요약
Merge Sort는 분할 정복 알고리즘의 하나이다.
분할 정복 알고리즘(Divide and Conquer) : 큰 문제를 2개의 작은 문제로 나눈 다음에 해결한 후 결과를 모아서 원래의 큰 문제를 해결하는 방식
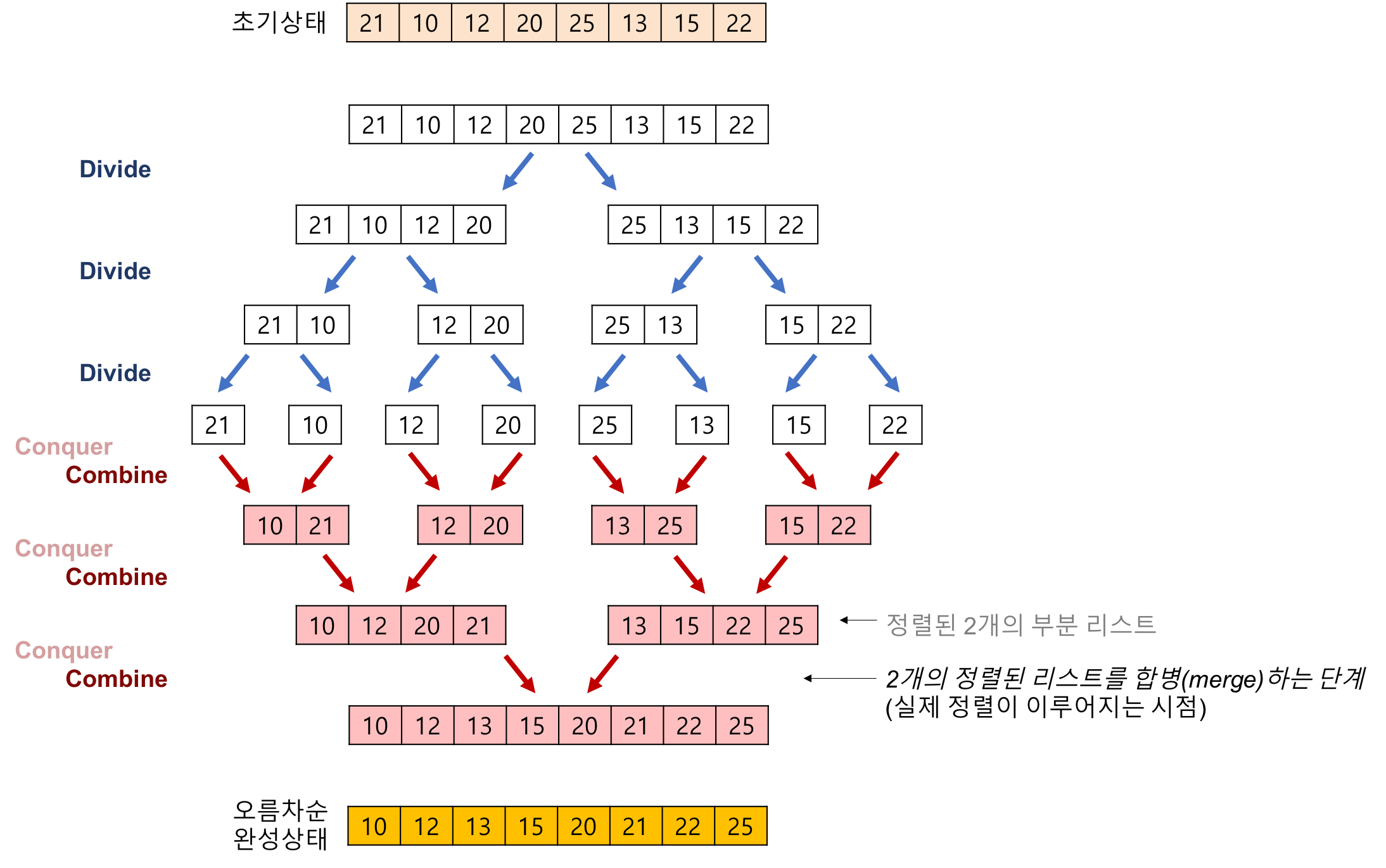
하나의 리스트를 균등하게 두 개의 리스트로 나눈 다음 정렬한 후, 두 개의 정렬된 리스트를 다시 합하여 정렬된 하나의 리스트로 만드는 방법이다.
Quick Sort가 피벗을 기준으로 정렬을 수행한 다음에 분할 한다면
Merge Sort는 분할을 먼저 하고 이후에 정렬을 수행한다.
과정 (오름차순)
- 리스트가 더이상 나뉘지 않을 때까지(리스트의 요소가 0개 혹은 1개) 분할을 진행한다.
- 두 개의 정렬된 리스트를 합병하는 과정을 반복 진행한다.
- 새로운 리스트를 생성한다.
- 2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 값 중 더 작은 값을 새로운 리스트에 추가한다.
- 요소를 추가한 리스트의 인덱스를 하나씩 추가하면서 비교를 반복 수행한다.
- 하나의 리스트가 먼저 끝난다면 남은 리스트의 값을 순서대로 넣어준다.
- 새로운 리스트를 기존의 리스트에 반영한다.
Kotlin 코드
fun mergeSort(array: MutableList<Int>, start: Int, end: Int) {
if (start >= end) return
val mid = (start + end) / 2
mergeSort(array, start, mid)
mergeSort(array, mid + 1, end)
merge(array, start, mid, end)
}
fun merge(array: MutableList<Int>, start: Int, mid:Int, end: Int) {
val newList = mutableListOf<Int>()
var idxA = start
var idxB = mid + 1
while (idxA <= mid && idxB <= end) {
if (array[idxA] <= array[idxB]) {
newList.add(array[idxA])
idxA++
} else {
newList.add(array[idxB])
idxB++
}
}
if (idxA > mid) {
for (i in idxB..end) {
newList.add(array[i])
}
}
if (idxB > end) {
for (i in idxA..mid) {
newList.add(array[i])
}
}
for (e in newList.indices) {
array[start + e] = newList[e]
}
}삽입정렬, 퀵정렬, 합병정렬 속도 비교
[5, 3, 8, 4, 9, 1, 6, 2, 7]
삽입 정렬 시간 : 1033900
퀵 정렬 시간 : 18791100
합병 정렬 시간 : 67000퀵 정렬이 전혀 빠르지 않다..(리스트의 교환 과정에서 많은 시간이 소요되는 것 같다.)
그래도 합병정렬이 삽입 정렬에 비해서 압도적으로 빠른 결과를 얻는 것은 확인하였다.
시간 복잡도
데이터의 분포에 상관없이 호출 깊이는 log n으로 동일하다.
- 각 합병 단계의 비교 연산(N) * 순환 호출의 깊이 만큼의 합병 단계(log N) = N log N
공간 복잡도
두 개의 정렬된 리스트를 합병하는 과정에서 임시 배열을 생성하여 사용한다면 O(N logN)
LinkedList를 활용한다면 O(N)
특징
장점
- 안정적인 정렬 방법이다.
- 데이터의 분포 상황에 상관없이 정렬되는 시간이 동일하다. (O(n*log n))
- 연결 리스트(Linked List)로 구현한다면 링크 인덱스만 변경되므로 데이터의 이동 연산 부담이 작아진다.
- 제자리 정렬로도 구현할 수 있다. (공간 복잡도 O(n))
- 따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 정렬 방법보다 효율적이다.
단점
- 구현이 다소 복잡하다.
- 리스트를 합병하는 과정에서 비교된 요소를 추가해놓는 임시 배열이 필요하다. (제자리 정렬이 아니다.)
- 리스트의 크기가 큰 경우에는 임시 배열을 생성하고 추가하고 원래의 배열로 옮기는 과정에서 시간이 많이 걸릴 수 있다.
LinkedList
- 인덱스를 통한 조회는 O(N)의 시간 복잡도를 가진다.
- 데이터의 삽입, 삭제에 대해서는 O(1)의 복잡도를 가진다.
- 데이터의 삽입, 삭제 연산이 많은 병합 정렬에서 성능이 좋음
- 데이터의 인덱스를 통한 조회가 잦은 퀵정렬에서 성능이 좋지 않음
Reference
반응형
'Programming > 알고리즘' 카테고리의 다른 글
| 기수 정렬 (Radix Sort) (1) | 2021.06.10 |
|---|---|
| 힙 정렬 (Heap Sort) (0) | 2021.06.07 |
| 퀵 정렬 (Quick Sort) (0) | 2021.06.01 |
| 삽입 정렬 (Insertion Sort) (0) | 2021.05.30 |
| 선택 정렬 (Selection Sort) (0) | 2021.05.30 |
댓글
