거품 정렬 (Bubble Sort)

거품 정렬 (Bubble Sort)

목표

• Bubble Sort에 대해 설명할 수 있다.
• Bubble Sort 과정에 대해 설명할 수 있다.
• Bubble Sort를 Kotlin으로 구현할 수 있다.
• Bubble Sort의 특징을 이해하여 시간 복잡도와 공간 복잡도를 계산할 수 있다.

요약

Bubble Sort는 인접한 두 원소의 대소 비교하여 조건에 충족하지 않으면 자리를 바꾸는 정렬 알고리즘이다.

정렬과정에서 요소가 천천히 정렬되는 모습이 거품이 수면 위로 떠오르는 것 같다고 해서 Bubble Sort라고 부른다.

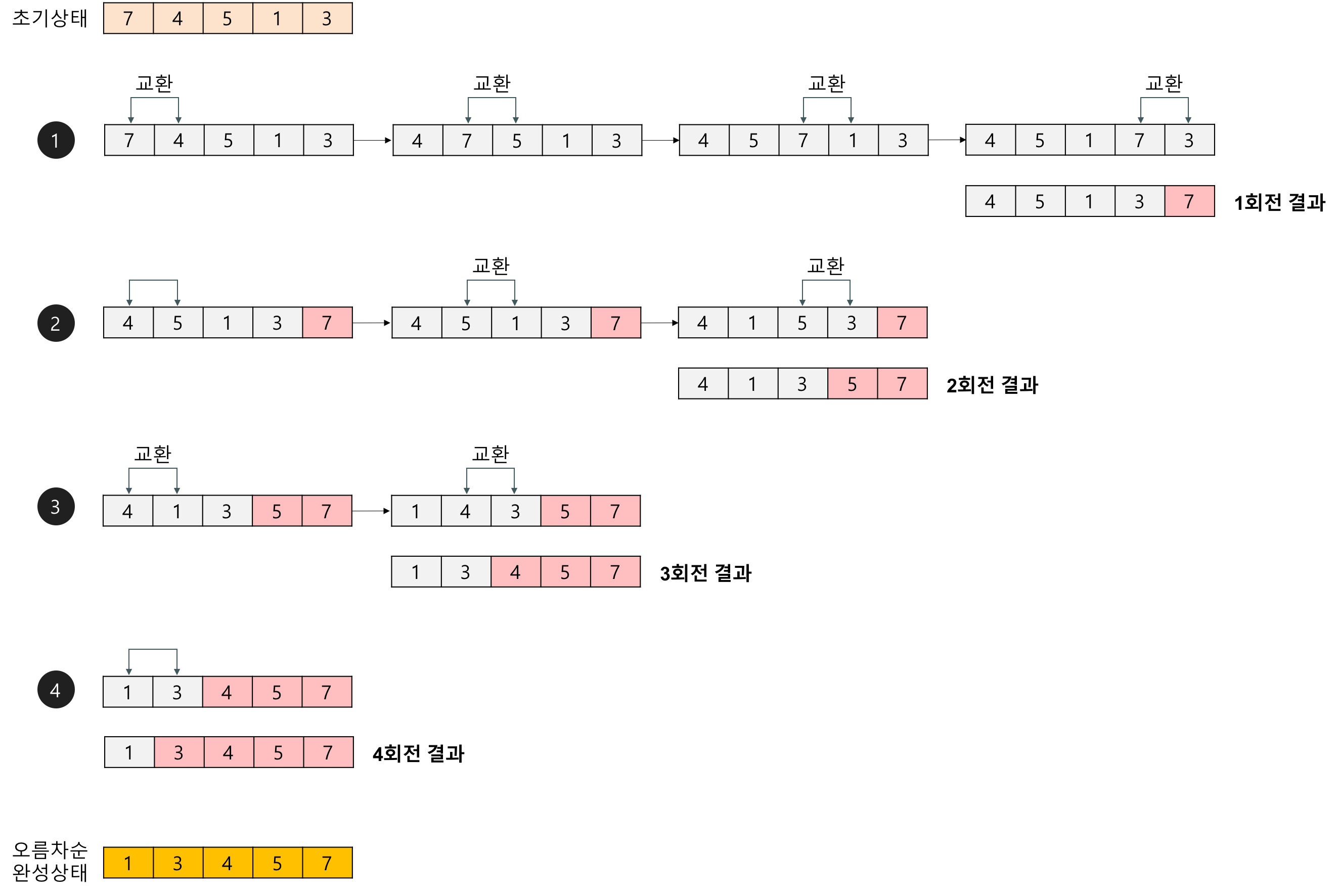
과정 (오름차순)

1. 첫 번째 요소와 두 번째 요소를 비교하여 앞의 요소가 더 크다면 두 요소의 위치를 교환(Swap)한다.
2. 1번 과정을 n-1번째 요소와 n번째 요소까지 반복하면 n번째에 가장 큰 요소가 배치되고 정렬에서 제외한다.
3. 다시 첫 번째 요소부터 n-1 번째까지 1번 과정을 반복하면 n-1번째에 두 번째로 큰 요소가 배치되고 정렬에서 제외한다.
4. 위 과정을 반복하면서 하나씩 정렬에서 제외하면 오름차순 정렬이 완료된다.

https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html

 

Kotlin 코드

val lst = mutableListOf(1, 34, 5, 6, 78, 23, 56, 31, 64)

fun bubbleSort() {
    for (i in lst.indices) {
        for (j in 0 until lst.count()-1-i) {
            if (lst[j] > lst[j + 1]) {
                val temp = lst[j]
                lst[j] = lst[j + 1]
                lst[j + 1] = temp
            }
        }
    }
    print(lst)
}

시간 복잡도

1회차에서 n-1번 비교, 2회차에서 n-2번 비교, n-1번차에서 1번 비교하므로 식은 다음과 같이 표현할 수 있다.

(n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2

Bubble Sort는 미리 정렬되어 있는지의 여부와 상관 없이 2개의 원소를 대소 비교하기 때문에 최선, 평균, 최악의 경우 모두 시간 복잡도가 O(n^2)로 동일하다.

공간 복잡도

기존에 주어진 배열에서 원소 Swap만 이루어지므로 공간 복잡도는 O(n)이다.

특징

장점

1. 구현이 매우 간단하고 직관적이다.
2. 주어진 배열에서만 교환하므로 다른 메모리 공간이 필요하지 않다. => 제자리 정렬(in-place sorting)
3. 안정 정렬(Stable Sort)이다. (https://godgod732.tistory.com/10)

단점

1. 시간 복잡도가 최선, 평균, 최악 모두 O(n^2)로 굉장히 비효율적이다.
2. 정렬되어 있지 않은 요소가 정렬 됐을 때의 자리로 가기 위해서 교환 연산이 빈번하게 일어난다.
3. 최종 정렬되었을 때의 위치에 이미 있는 요소도 교환되는 일이 있다.

Reference

• https://github.com/GimunLee/tech-refrigerator/blob/master/Algorithm/%EA%B1%B0%ED%92%88%20%EC%A0%95%EB%A0%AC%20(Bubble%20Sort).md#%EA%B1%B0%ED%92%88-%EC%A0%95%EB%A0%AC-bubble-sort
• https://godgod732.tistory.com/10
• https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html