티스토리 뷰
하노이의 탑
하노이의 탑이라는 단어는 뭔가 익숙했는데 문제 내용은 굉장히 생소한 내용이었습니다. 재귀 문제를 설명하는 데 있어서 많이 다룬다고 하는데 비전공자여서 그런가 이런 문제가 낯설기만 합니다..
그래서 가끔 이런 유명한 문제에 대해서는 포스팅을 하면서 깊게 파야겠습니다.
문제 설명
'하노이의 탑'은 프랑스의 수학자 에두아르 뤼카가 1883년 소개한 유명한 문제로 다음과 같이 그림으로 표현할 수 있습니다.

이 문제의 목표는 기둥 A에 쌓여 있는 원판을 기둥 C에 옮겨서 다시 쌓는 것이 목표입니다.
하지만 원판을 옮길 시에는 다음과 같은 두 가지 조건을 만족하면서 옮겨져야 합니다.
- 한 번에 하나의 원판만 옮길 수 있습니다.
- 큰 원판이 작은 원판 위에 있어서는 안됩니다.
이 조건에서 '최소의 이동횟수로 옮기는 가짓 수'나 '최소의 이동횟수로 옮길 때 각 원판을 옮기는 순서'등을 구하는 것이 하노이의 탑 문제가 됩니다. 우리는 '최소의 이동횟수로 옮길 때 각 원판을 옮기는 순서'를 구해보도록 합시다.
문제 아이디어
문제의 아이디어를 얻기 전에 우리는 이 문제가 재귀와 관련되어 있음을 알지 못한다. 우리는 어떻게 '하노이의 탑'을 풀 수 있는 아이디어를 얻을 수 있을까? 어떤 알고리즘 문제든 아이디어가 번뜩이지 않을 때는 직접 원판을 옮겨 보는 것이 좋다! 그리고 작은 문제를 만들어 해결한 다음에 조금 더 큰 문제로 확대시켜 나가면서 접근하는 것이다. (적고 보니 약간 DP 문제 해결법과 일맥상통하는 것 같다.)

원판이 3개인 하노이의 탑 문제는 총 7개의 과정을 통해서 A 기둥에서 C 기둥으로 원판을 옮길 수 있다. 그 과정은 다음과 같습니다.
1. 1번 원반을 A에서 C로 이동
2. 2번 원반을 A에서 B로 이동
3. 1번 원반을 C에서 B로 이동
4. 3번 원반을 A에서 C로 이동
5. 1번 원반을 B에서 A로 이동
6. 2번 원반을 B에서 C로 이동
7. 1번 원반을 A에서 C로 이동위 과정은 3가지 단계로 나눌 수 있습니다.
1~3 단계 : A 기둥에 있는 1, 2번 원판을 B 기둥으로 옮기는 과정
4단계 : A 기둥에 있는 3번 원판을 C 기둥으로 옮기는 과정
5~7 단계 : B 기둥에 있는 1, 2번 원판을 C 기둥으로 옮기는 과정
3개의 원판을 옮기는 과정 중에서 2개의 원판을 옮기는 과정 2개(1
3, 5
7)를 찾아볼 수 있습니다.
이는 원판이 N개 있을 때도 성립하는 규칙이며 식으로 나타내면 다음과 같습니다.
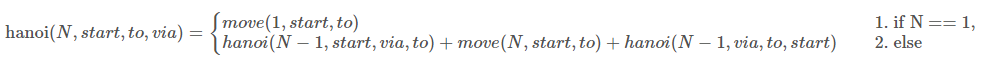
위 재귀식을 구현하는 데 있어서 필요한 인자는 다음과 같습니다.
- 원판의 개수
- 시작 기둥 번호
- 도착 기둥 번호
- 나머지 기둥 번호
더 자세한 내용은 아래 포스팅에서 확인해주세요.
https://shoark7.github.io/programming/algorithm/tower-of-hanoi
코드
class Solution {
fun solution(n: Int): Array<IntArray> {
var answer = mutableListOf<IntArray>()
fun hanoi(num: Int, start: Int, end: Int, via: Int) {
if (num == 1) {
answer.add(intArrayOf(start, end))
return
}
hanoi(num - 1, start, via, end)
answer.add(intArrayOf(start, end))
hanoi(num - 1, via, end, start)
}
hanoi(n, 1, 3, 2)
return answer.toTypedArray()
}
}대체로 위의 내용을 그대로 구현하였고 원판의 개수가 1일 때는 원판을 옮기고 hanoi함수를 바로 return합니다.
'알고리즘 문제 풀이 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 가장 큰 수 (0) | 2020.12.18 |
|---|---|
| [프로그래머스] K번째 수 (0) | 2020.12.18 |
| [프로그래머스] 카펫 (0) | 2020.12.17 |
| [프로그래머스] 소수 찾기 (0) | 2020.12.16 |
| [프로그래머스] 모의고사 (0) | 2020.12.16 |
